<!–more–>
前言
数据结构和算法的知识博大精深, 这里只是对这几种数据结构做一些简单的介绍。并对leetcode上部分相关的简单和中等题做出解答。还请各位看官见谅
二叉树
二叉树是一种典型的树状结构, 二叉树每一个节点最多有两个子树的结构。以下是遍历二叉树的几种方式, 总的来说使用递归的方式, 还是非常好理解的。
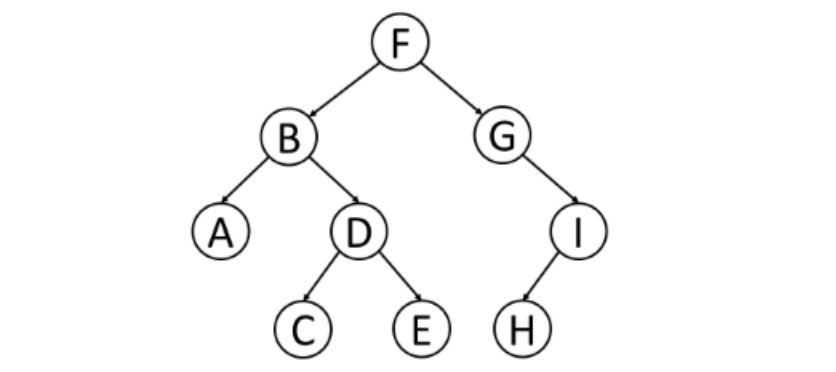
深度优先遍历 前序遍历
前序遍历首先访问根节点,然后遍历左子树,最后遍历右子树
节点遍历的顺序: F, B, A, D, C, E, G, I, H
var preorderTraversal = function (root) {
let result = []
const traversing = (node) => {
// 结束递归
if (!node) return []
// 首先遍历当前的节点
result.push(node.val)
// 如果有左子树优先遍历左子树
if (node.left) {
result.concat(traversing(node.left))
}
// 遍历又子树
if (node.right) {
result.concat(traversing(node.right))
}
}
traversing(root)
return result
}
深度优先遍历 中序遍历
中序遍历是先遍历左子树,然后访问根节点,然后遍历右子树
节点遍历的顺序: A, B, C, D, E, F, G, H, I
var inorderTraversal = function (root) {
let result = []
const traversing = (node) => {
if (!node) return
// 优先遍历左子树
if (node.left) {
traversing(node.left)
}
// 然后获取当前的节点
if (node.val) {
result.push(node.val)
}
// 然后遍历右子树
if (node.right) {
traversing(node.right)
}
}
traversing(root)
return result
}
深度优先遍历 后序遍历
先遍历左子树,然后遍历右子树,最后访问树的根节点
节点遍历的顺序: A, C, E, D, B, H, I, G, F
var postorderTraversal = function (root) {
let result = []
const traversing = (node) => {
if (!node) return
if (node.left) {
traversing(node.left)
}
if (node.right) {
traversing(node.right)
}
if (node.val) {
result.push(node.val)
}
}
traversing(root)
return result
};
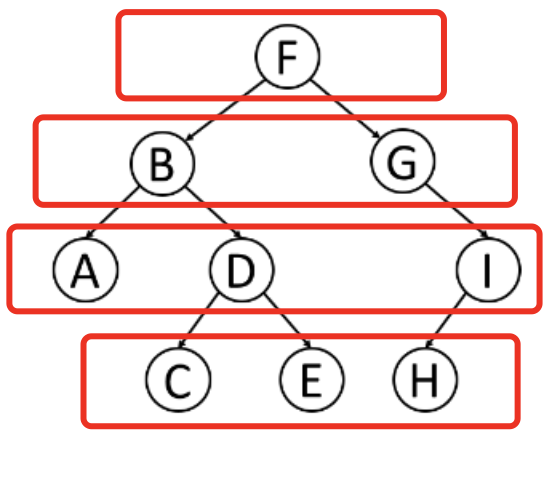
广度优先遍历
广度优先搜索是一种广泛运用在树或图这类数据结构中,遍历或搜索的算法。该算法从一个根节点开始,首先访问节点本身。然后依次遍历它的二级邻节点、三级邻节点,以此类推。我们这里依然使用递归遍历, 但是我们在递归中添加level参数用来确定当前节点的层级。
var levelOrder = function (root) {
let result = []
const traversing = (node, level) => {
if (!node) return
if (!result[level]) result[level] = []
result[level].push(node.val)
if (node.left) {
traversing(node.left, level + 1)
}
if (node.right) {
traversing(node.right, level + 1)
}
}
traversing(root, 0)
return result
}
二叉树的最大深度
题目
给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
思路
对当前的二叉树使用后序遍历。如果当前节点没有左子树并且没有右子树, 说明这个节点是当前分支中最深的节点, 我们记录它自身的最大深度为1(因为它自身没有子节点)。如果当前节点有左子树和右子树, 我们取左右子树中最大的深度(因为是后序遍历, 在遍历当前根节点时, 左右树已经被遍历了)。取最大深度后加一就是当前节点的深度。
解答
var maxDepth = function(root) {
if (!root) return 0
const traversing = (node) => {
if (!node) return
if (!node.left && !node.right) {
node.depth = 1
return
}
if (node.left) {
traversing(node.left)
}
if (node.right) {
traversing(node.right)
}
let max_left_depth = 0
let max_right_depth = 0
if (node.left) {
max_left_depth = node.left.depth
}
if (node.right) {
max_right_depth = node.right.depth
}
node.depth = Math.max(max_left_depth, max_right_depth) + 1
}
traversing(root)
return root.depth
}
对称二叉树
给定一个二叉树,检查它是否是镜像对称的
// 对称二叉树
1
/ \
2 2
/ \ / \
3 4 4 3
// 不是对称二叉树
1
/ \
2 2
\ \
3 3
思路
采用BFS遍历, 获取每一级的所有节点结果集, 不存在的子节点使用null代替。判断每一级的节点是否能构成回文字符串即可。
解答
var isSymmetric = function(root) {
// BFS遍历
let result = []
const traversing = (node, level) => {
if (!result[level]) result[level] = []
// 不存在的节点使用null填充
if (!node) {
// 终止递归
return result[level].push('null')
} else {
result[level].push(node.val)
}
if (node.left) {
traversing(node.left, level + 1)
} else {
traversing(null, level + 1)
}
if (node.right) {
traversing(node.right, level + 1)
} else {
traversing(null, level + 1)
}
}
traversing(root, 0)
// 判断每一级的结果能否构成回文字符串
for (let i = 0; i < result.length - 1; i++) {
if (result[i].join('') !== result[i].reverse().join('')) {
return false
}
}
return true
};
路径总和
题目
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
// 给定目标sum = 22
// 5->4->11->2和为22, 返回true
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
思路
我们采用前序遍历, 每次遍历使用目标减去当前节点的值,并将新的目标带入下一次的递归中。如果当遍历到最深处的节点,并且节点的值等于目标的值。说明二叉树拥有路径的和等于目标值。
解答
var hasPathSum = function(root, sum) {
let result = []
const traversing = (root, sum) => {
if (!root) return false
// 说明拥有路径等于目标的和
if (!root.left && !root.right && root.val === sum) {
result.push(root.val)
}
if (root.left) {
traversing(root.left, sum - root.val)
}
if (root.right) {
traversing(root.right, sum - root.val)
}
}
traversing(root, sum)
return result.length > 0
};
从中序与后序遍历序列构造二叉树
题目
根据一棵树的中序遍历与后序遍历构造二叉树。
// 中序遍历 inorder = [9,3,15,20,7]
// 后序遍历 postorder = [9,15,7,20,3]
// 构建结果
3
/ \
9 20
/ \
15 7
思路
思路与从前序与中序遍历序列构造二叉树题类似,这里不在赘述
解答
var buildTree = function(inorder, postorder) {
let binaryTree = {}
const iteration = (postorder, inorder, tree) => {
if (!postorder.length) {
binaryTree = null
return
}
tree.val = null
tree.left = {
val: null,
left: null,
right: null
}
tree.right = {
val: null,
left: null,
right: null
}
// 前序遍历第一个节点为当前树的根节点
let rootVal = postorder.splice(postorder.length - 1, 1)[0]
// 中序遍历根节点的索引
let rootIndex = inorder.indexOf(rootVal)
// 中序遍历的左子树
let inorderLeftTree = inorder.slice(0, rootIndex)
// 中序遍历的右子树
let inorderRightTree = inorder.slice(rootIndex + 1)
// 前序遍历的左子树
let postorderLeftTree = postorder.slice(0, inorderLeftTree.length)
// 前序遍历的右子树
let postorderRightTree = postorder.slice(inorderLeftTree.length)
tree.val = rootVal
if (postorderLeftTree.length === 1 || inorderLeftTree.length === 1) {
tree.left.val = postorderLeftTree[0]
} else if (postorderLeftTree.length > 1 || inorderLeftTree.length > 1) {
iteration(postorderLeftTree, inorderLeftTree, tree.left)
} else {
tree.left = null
}
if (postorderRightTree.length === 1 || inorderRightTree.length === 1) {
tree.right.val = postorderRightTree[0]
} else if (postorderRightTree.length > 1 || inorderRightTree.length > 1) {
iteration(postorderRightTree, inorderRightTree, tree.right)
} else {
tree.right = null
}
}
iteration(postorder, inorder, binaryTree)
return binaryTree
}
从前序与中序遍历序列构造二叉树
思路
本题依然采用递归的思路, 前序遍历的第一个节点为二叉树的根节点,以此作为突破口。
本题的前置条件是树中不存在重复的元素。可以由中序遍历的结果以及根节点值获取根节点的左子树以及右子树。
我们这时可以获得根节点左子树和右子树的长度。反过来可以获取前序遍历结果中的左右子树。我们这时,把左右子树再当成一颗二叉树,使用递归的形式重复此过程。既可以推导出整颗二叉树。
解答
var buildTree = function(preorder, inorder) {
let binaryTree = {}
const iteration = (preorder, inorder, tree) => {
if (!preorder.length) {
binaryTree = null
return
}
tree.val = null
tree.left = {
val: null,
left: null,
right: null
}
tree.right = {
val: null,
left: null,
right: null
}
// 前序遍历第一个节点为当前树的根节点
let rootVal = preorder.splice(0, 1)[0]
// 中序遍历根节点的索引
let rootIndex = inorder.indexOf(rootVal)
// 中序遍历的左子树
let inorderLeftTree = inorder.slice(0, rootIndex)
// 中序遍历的右子树
let inorderRightTree = inorder.slice(rootIndex + 1)
// 前序遍历的左子树
let preorderLeftTree = preorder.slice(0, inorderLeftTree.length)
// 前序遍历的右子树
let preorderRightTree = preorder.slice(inorderLeftTree.length)
tree.val = rootVal
if (preorderLeftTree.length === 1 || inorderLeftTree.length === 1) {
tree.left.val = preorderLeftTree[0]
} else if (preorderLeftTree.length > 1 || inorderLeftTree.length > 1) {
iteration(preorderLeftTree, inorderLeftTree, tree.left)
} else {
tree.left = null
}
if (preorderRightTree.length === 1 || inorderRightTree.length === 1) {
tree.right.val = preorderRightTree[0]
} else if (preorderRightTree.length > 1 || inorderRightTree.length > 1) {
iteration(preorderRightTree, inorderRightTree, tree.right)
} else {
tree.right = null
}
}
iteration(preorder, inorder, binaryTree)
return binaryTree
}
二叉搜索树
二叉搜索树是二叉树的一种特殊形式。 二叉搜索树具有以下性质:每个节点中的值必须大于(或等于)其左侧子树中的任何值,但小于(或等于)其右侧子树中的任何值。
对于二叉搜索树,我们可以通过中序遍历得到一个递增的有序序列
验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
思路
可以通过中序DFS遍历二叉搜索树, 判断遍历的结果是否为递增的数组判断是否为搜索二叉树
解答
var isValidBST = function(root) {
if (!root) return true
// 中序DFS
let result = []
const iteration = (root) => {
if (root.left) {
iteration(root.left)
}
result.push(root.val)
if (root.right) {
iteration(root.right)
}
}
iteration(root)
let resultString = result.join(',')
let result2String = [...new Set(result.sort((a, b) => a - b))].join(',')
return resultString === result2String
};
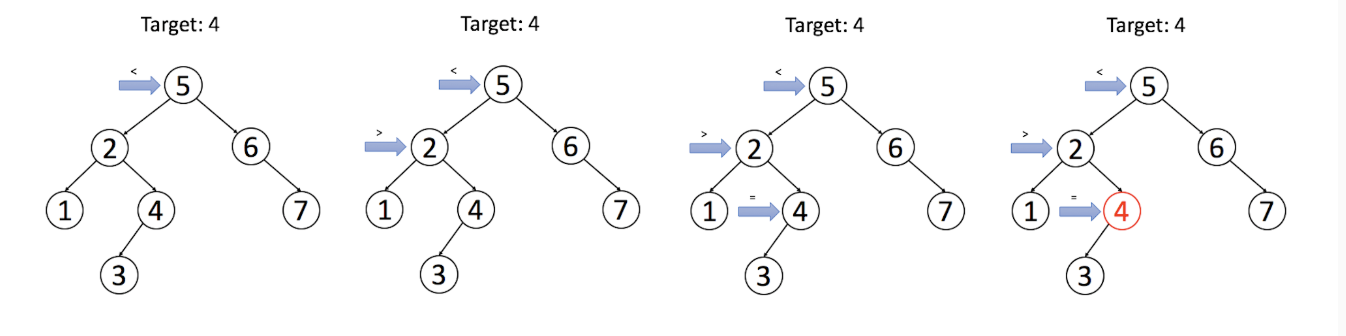
在二叉搜索树中实现搜索操作
如果目标值等于节点的值,则返回节点, 如果目标值小于节点的值,则继续在左子树中搜索, 如果目标值大于节点的值,则继续在右子树中搜索。
// 递归就完事了
var searchBST = function(root, val) {
if (!root) return null
let result = null
const seatch = (node) => {
if (node.val === val) {
return result = node
} else if (val > node.val && node.right) {
seatch(node.right)
} else if (val < node.val && node.left) {
seatch(node.left)
}
}
seatch(root)
return result
};
在二叉搜索树中实现插入操作
在二叉搜索树中的插入操作和搜索操作类似。根据节点值与目标节点值的关系,搜索左子树或右子树。当节点没有左右子树时。判断目标值和当前节点的关系,执行插入的操作。
var insertIntoBST = function(root, val) {
const insert = (root) => {
if (val > root.val) {
if (root.right) {
insert(root.right)
} else {
root.right = new TreeNode(val)
}
} else if (val < root.val) {
if (root.left) {
insert(root.left)
} else {
root.left = new TreeNode(val)
}
}
}
insert(root)
return root
};
在二叉搜索树中实现删除操作
删除二叉树的节点的操作复杂度远远大于搜索和插入的操作。删除搜索二叉树节点时, 需要考虑多种状态
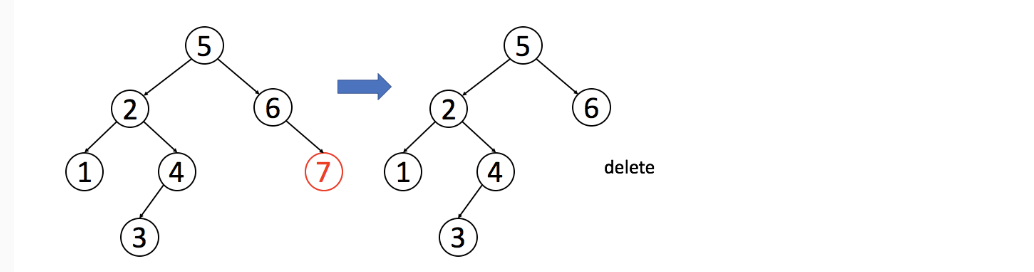
删除的节点没有子节点的时候, 直接移除改节点(从它的父节点上移除)
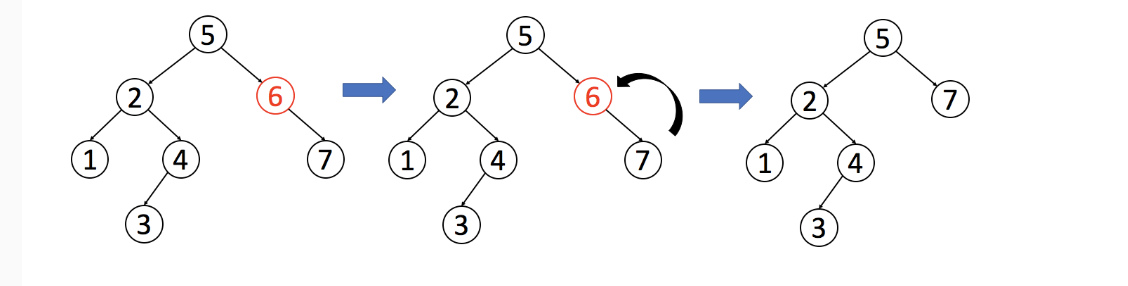
删除的节点只有一个子节点的时候, 需要将需要删除的节点的父节点, 链接上删除节点的子节点。即可完成删除
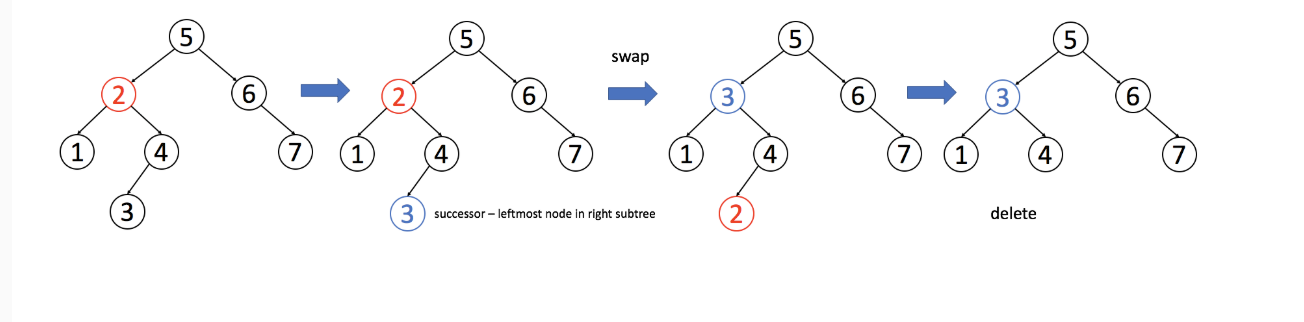
删除的节点有两个子节点的时候, 需要将删除节点右子树中的最小值, 赋予删除的节点。然后删除右子树中的最小值即可。
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {number} key
* @return {TreeNode}
*/
var deleteNode = function(root, key) {
// 根节点为空的情况
if (!root) {
return null
}
if (!root.left && !root.right && root.val === key) {
root = null
return root
}
if (!root.left && root.right && root.val === key) {
root = root.right
return root
}
if (root.left && !root.right && root.val === key) {
root = root.left
return root
}
// 根节点替换的情况
// 寻找当前树的最小节点
const findMin = (root) => {
let min = root
while (min.left) {
min = min.left
}
return min
}
let parentNode = null
// 找到最近的父级
const searchParent = (node, searchValue) => {
console.log('???')
let current = node
let breaker = false
while (!breaker) {
console.log('查找父亲')
if (
(current.left && searchValue === current.left.val) ||
(current.right && searchValue === current.right.val)
) {
breaker = true
} else if (searchValue < current.val) {
current = current.left
} else if (searchValue > current.val) {
current = current.right
} else {
current = null
}
if (!current) break
}
parentNode = current
}
const remove = (node, deleteValue) => {
if (node.val === deleteValue) {
console.log('1')
// node为要删除的节点
if (!node.left && !node.right) {
console.log('3')
// 如果没有任何子节点
searchParent(root, node.val)
if (parentNode.left && parentNode.left.val === deleteValue) {
parentNode.left = null
} else {
parentNode.right = null
}
} else if (!node.left && node.right) {
console.log('4')
// 如果只有一个子节点
searchParent(root, node.val)
if (parentNode.left && parentNode.left.val === deleteValue) {
parentNode.left = node.right
} else {
parentNode.right = node.right
}
} else if (node.left && !node.right) {
console.log('5')
// 如果只有一个子节点
searchParent(root, node.val)
if (parentNode.left && parentNode.left.val === deleteValue) {
parentNode.left = node.left
} else {
parentNode.right = node.left
}
} else {
console.log('6')
// 如果有两个子节点
// 找到右子树中最小的节点
let minNode = findMin(node.right)
console.log('7')
let minNodeValue = minNode.val
console.log('8')
remove(root, minNodeValue)
console.log('9')
node.val = minNodeValue
console.log('10')
}
} else if (deleteValue > node.val && node.right) {
console.log('2')
remove(node.right, deleteValue)
} else if (deleteValue < node.val && node.left) {
console.log('3')
remove(node.left, deleteValue)
}
}
remove(root, key)
return root
};
二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
思路
从根节点开始遍历操作, 如果根节点的值大于目标节点1, 小于目标节点2。说明根节点就是最近的公共祖先。
如果根节点大于目标节点1, 目标节点2,则使用根节点的左子节点重复前一步的操作。
如果根节点小于目标节点1, 目标节点2,则使用根节点的右子节点重复前一步的操作。
解答
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function(root, p, q) {
if (root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left, p, q)
}
if (root.val < p.val && root.val < q.val) {
return lowestCommonAncestor(root.right, p, q)
}
return root
};
前缀树
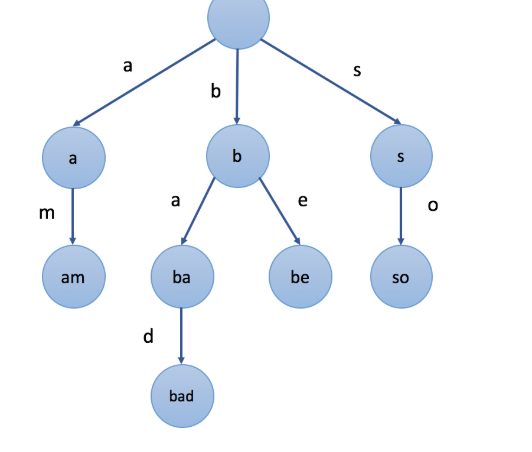
前缀树是N叉树的一种特殊形式。前缀树的每一个节点通常表示一个字符或者字符串。每一个节点拥有多个不同的子节点。值得注意的是,根节点表示空字符串。
前缀树的一个重要的特性是,节点所有的后代都与该节点相关的字符串有着共同的前缀。这就是前缀树名称的由来。
如何表示一个Trie树?
方法1, 使用长度为26的数组存储子节点
方法2, 使用hashMap存储子节点
实现 Trie (前缀树)
var TrieNode = function (val = null) {
// 当前的值
this.val = val
// 当前节点的子节点
this.children = {}
// 表示当前节点是否为一个单词
this.isWord = false
}
// 添加到节点
TrieNode.prototype.add = function (val) {
let child = new TrieNode(val)
this.children[val] = child
return this.children[val]
}
// 判断是否包含子节点
TrieNode.prototype.has = function (val) {
return this.children[val] ? true : false
}
/**
* Initialize your data structure here.
*/
var Trie = function() {
// 初始化根节点
this.root = new TrieNode('')
};
/**
* Inserts a word into the trie.
* @param {string} word
* @return {void}
*/
Trie.prototype.insert = function(word) {
let current = this.root
let words = word.split('')
let i = 0
// 替换最后一个节点
while (i < words.length) {
if (!current.has(words[i])) {
// 如果不存在该子节点
current = current.add(words[i])
} else {
// 如果存在该子节点
current = current.children[words[i]]
}
i += 1
}
current.isWord = true
};
/**
* Returns if the word is in the trie.
* 判断是否存在单词
* @param {string} word
* @return {boolean}
*/
Trie.prototype.search = function(word) {
let current = this.root
let words = word.split('')
let i = 0
let result = null
while (i < words.length) {
if (current.has(words[i])) {
current = current.children[words[i]]
i += 1
} else {
return false
}
}
return current.isWord
};
/**
* Returns if there is any word in the trie that starts with the given prefix.
* 判断是否包含单词
* @param {string} prefix
* @return {boolean}
*/
Trie.prototype.startsWith = function(prefix) {
let current = this.root
let prefixs = prefix.split('')
let i = 0
while (i < prefixs.length) {
if (current.has(prefixs[i])) {
current = current.children[prefixs[i]]
i += 1
} else {
return false
}
}
return true
};
/**
* Your Trie object will be instantiated and called as such:
* var obj = Object.create(Trie).createNew()
* obj.insert(word)
* var param_2 = obj.search(word)
* var param_3 = obj.startsWith(prefix)
*/
单词替换
在英语中,我们有一个叫做 词根(root)的概念,它可以跟着其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如,词根an,跟随着单词 other(其他),可以形成新的单词 another(另一个)。
现在,给定一个由许多词根组成的词典和一个句子。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根,则用最短的词根替换它。
输入: dict(词典) = [“cat”, “bat”, “rat”]
sentence(句子) = “the cattle was rattled by the battery”
输出: “the cat was rat by the bat”
思路
解答
var replaceWords = function(dict, sentence) {
let sentences = sentence.split(' ')
let result = []
for (let i = 0; i < sentences.length; i++) {
let trie = new Trie()
// 句子中的每一个词形成一个前缀树
trie.insert(sentences[i])
let min = sentences[i]
for (let j = 0; j < dict.length; j++) {
// 判断是否包含词根
if (trie.startsWith(dict[j])) {
// 取最短的词根
min = min.length < dict[j].length ? min : dict[j]
}
}
result.push(min)
}
return result.join(' ')
};
N叉树
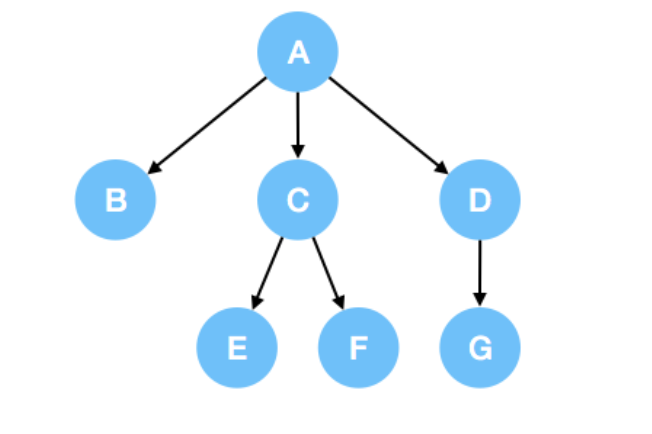
N叉树的前序遍历
先访问根节点,然后以此遍历根节点的所有子节点。如果子节点存在子节点。同根节点一样,先遍历自身然后遍历它的子节点。
var preorder = function(root) {
let result = []
const iteration = (root) => {
if (!root) return
result.push(root.val)
if (root.children) {
for (let i = 0; i < root.children.length; i++) {
iteration(root.children[i])
}
}
}
iteration(root)
return result
}
N叉树的后序遍历
优先遍历根节点的所有子节点,如果子节点存在子节点,则优先遍历其它的子节点
var postorder = function(root) {
let result = []
const iteration = (root) => {
if (!root) return
if (root.children) {
for (let i = 0; i < root.children.length; i++) {
iteration(root.children[i])
}
}
result.push(root.val)
}
iteration(root)
return result
};
N叉树的层序遍历
var levelOrder = function (root) {
let reuslt = []
const iteration = (root, level) => {
if (!root) return
if (!reuslt[level]) {
reuslt[level] = []
}
reuslt[level].push(root.val)
for (let i = 0; i < root.children.length; i++) {
iteration(root.children[i], level + 1)
}
}
iteration(root, 0)
return reuslt
};
N叉树最大深度
给定一个 N 叉树,找到其最大深度。最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
思路
思路很简单, BFS整个N叉树, 返回结果的长度即可
解答
var maxDepth = function(root) {
let reuslt = []
const iteration = (root, level) => {
if (!root) return
if (!reuslt[level]) {
reuslt[level] = []
}
reuslt[level].push(root.val)
for (let i = 0; i < root.children.length; i++) {
iteration(root.children[i], level + 1)
}
}
iteration(root, 0)
return reuslt.length
};



