Introduction

面试过程通常从最初的电话面试开始，然后是现场面试，检查编程技能和文化契合度。几乎毫无例外，最终的决定因素是还是编码能力。通常上，不仅仅要求能得到正确的答案，更重要的是要有清晰的思维过程。写代码中就像在生活中一样，正确的答案并不总是清晰的，但是好的推理通常就足够了。有效推理的能力预示着学习、适应和进化的潜力。好的工程师一直是在成长的，好的公司总是在创新的。

算法挑战是有用的，因为解决它们的方法不止一种。这为决策的制定和决策的计算提供了可能性。在解决算法问题时，我们应该挑战自己从多个角度来看待问题的定义，然后权衡各种方法的优缺点。通过足够的尝试后，我们甚至可能看到一个普遍的真理:不存在“完美”的解决方案。

要真正掌握算法，就必须了解它们与数据结构的关系。数据结构和算法就像阴阳、水杯和水一样密不可分。没有杯子，水就不能被容纳。没有数据结构，我们就没有对象来应用逻辑。没有水，杯子是空的，没有营养。没有算法，对象就不能被转换或“消费”。

要了解和分析JavaScript中的数据结构，请看JavaScript中的数据结构

Primer

在JavaScript中，算法只是一个函数，它将某个确定的数据结构输入转换为某个确定的数据结构输出。函数内部的逻辑决定了怎么转换。首先，输入和输出应该清楚地提前定义。这需要我们充分理解手上的问题，因为对问题的全面分析可以很自然地提出解决方案，而不需要编写任何代码。

一旦完全理解了问题，就可以开始对解决方案进行思考，需要那些变量？ 有几种循环？ 有那些JavaScript内置方法可以提供帮助？需要考虑那些边缘情况？复杂或者重复的逻辑会导致代码十分的难以阅读和理解，可以考虑能否提出抽象成多个函数？一个算法通常上需要可扩展的。随着输入size的增加，函数将如何执行? 是否应该有某种缓存机制吗? 通常上，需要牺牲内存优化(空间)来换取性能提升(时间)。

为了使问题更加具体，画图表！

当解决方案的具体结构开始出现时，伪代码就可以开始了。为了给面试官留下深刻印象，请提前寻找重构和重用代码的机会。有时，行为相似的函数可以组合成一个更通用的函数，该函数接受一个额外的参数。其他时候，函数柯里的效果更好。保证函数功能的纯粹方便测试和维护也是非常重要的。换句话说，在做出解决问题的决策时需要考虑到架构和设计模式。

Big O（复杂度）

为了计算出算法运行时的复杂性，我们需要将算法的输入大小外推到无穷大，从而近似得出算法的复杂度。最优算法有一个恒定的时间复杂度和空间复杂度。这意味着它不关心输入的数量增长多少，其次是对数时间复杂度或空间复杂度，然后是线性、二次和指数。最糟糕的是阶乘时间复杂度或空间复杂度。算法复杂度可用以下符号表示:

1. Constabt: O(1)
2. Logarithmic: O(log n)
3. Linear: O(n)
4. Linearithmic: O(n log n)
5. Quadratic: O(n^2)
6. Expontential: O(2^n)
7. Factorial: O(n!)

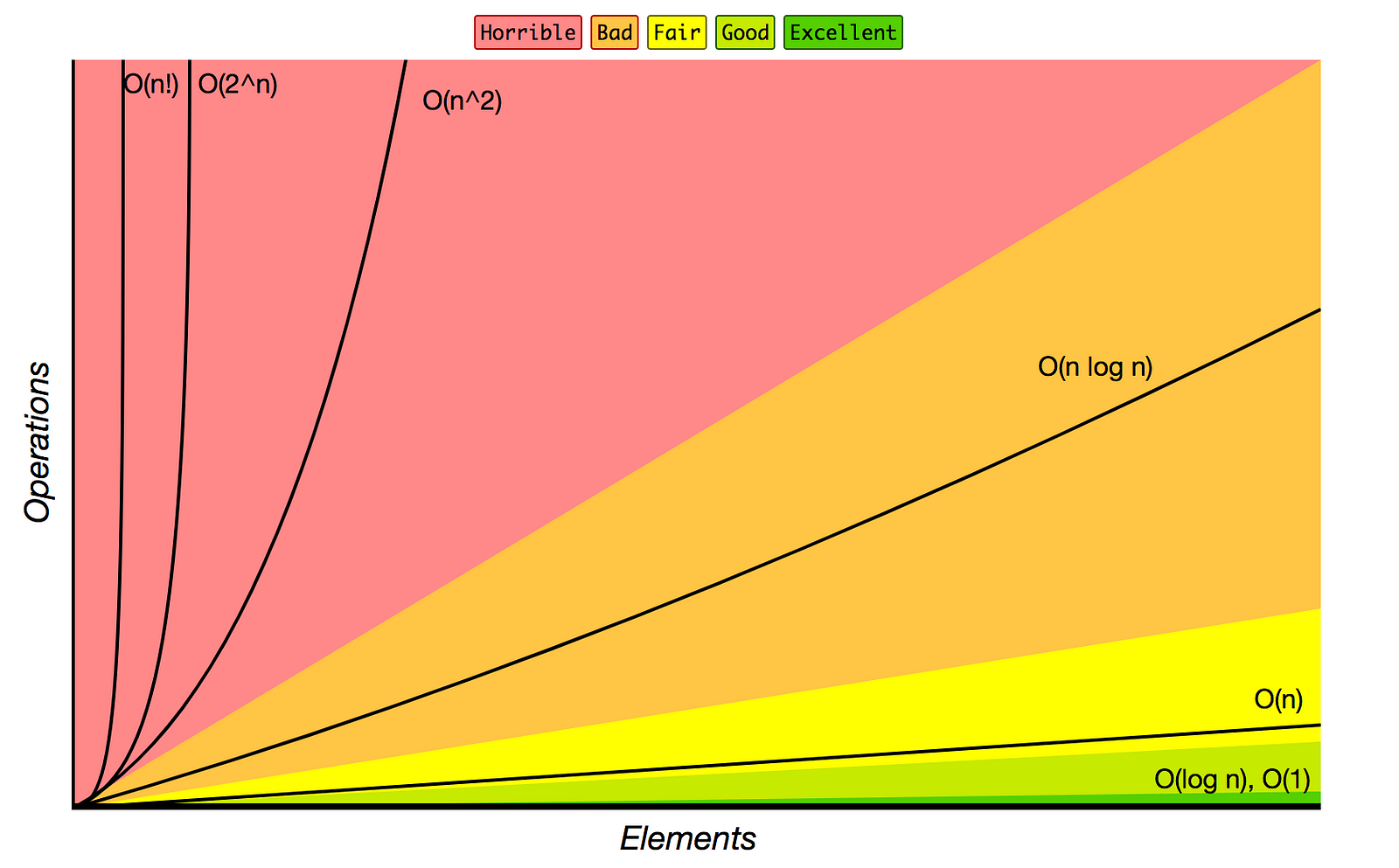
在设计算法的结构和逻辑时，时间复杂度和空间复杂度的优化和权衡是一个重要的步骤。

Arrays

一个最优的算法通常上会利用语言里固有的标准对象实现。可以说，在计算机科学中最重要的是数组。在JavaScript中，没有其他对象比数组拥有更多的实用方法。值得记住的数组方法有:sort、reverse、slice和splice。数组元素从第0个索引开始插入，所以最后一个元素的索引是 array.length-1。数组在push元素有很好的性能，但是在数组中间插入，删除和查找元素上性能却不是很优，JavaScript中的数组的大小是可以动态增长的。

数组的各种操作复杂度

• Push: O(1)
• Insert: O(n)
• Delet: O(n)
• Searching: O(n)
• Optimized Searching: O(log n)

Map 和 Set是和数组相似的数据结构。set中的元素都是不重复的，在map中，每个Item由键和值组成。当然，对象也可以用来存储键值对，但是键必须是字符串。

Iterations

与数组密切相关的是使用循环遍历它们。在JavaScript中,有5种最常用的遍历方法，使用最多的是for循环，for循环可以用任何顺序遍历数组的索引。如果无法确定迭代的次数，我们可以使用while和do while循环，直到满足某个条件。对于任何Object, 我们可以使用 for in 和 for of循环遍历它的keys 和values。为了同时获取key和value我们可以使用 entries()。我们也可以在任何时候使用break语句终止循环，或者使用continue语句跳出本次循环进入下一次循环。

原生数组提供了如下迭代方法：indexOf,lastIndexOf,includes,fill,join。 另外我们可以提供一个回调函数在如下方法中：findIndex,find,filter,forEach,map,some,every,reduce。

Recursions

在一篇开创性的论文中，Church-Turing论文证明了任何迭代函数都可以用递归函数来复制，反之亦然。有时候，递归方法更简洁、更清晰、更优雅。以这个迭代阶乘函数为例:

const factorial = number => {
  let product = 1
  for (let i = 2; i <= number; i++) {
    product *= i
  }
  return product
}

如果使用递归，仅仅需要一行代码

const _factorial = number => {
  return number < 2 ? 1 : number * _factorial(number - 1)
}

所有的递归函数都有相同的模式。它们由创建一个调用自身的递归部分和一个不调用自身的基本部分组成。任何时候一个函数调用它自身都会创建一个新的执行上下文并推入执行栈顶直。这种情况会一直持续到直到满足了基本情况为止。然后执行栈会一个接一个的将栈顶元素推出。因此，对递归的滥用可能导致堆栈溢出的错误。

最后，我们一起来思考一些常见算法题！

1. 字符串反转

一个函数接受一个字符串作为参数，返回反转后的字符串

describe("String Reversal", () => {
 it("Should reverse string", () => {
  assert.equal(reverse("Hello World!"), "!dlroW olleH");
 })
})

思考

这道题的关键点是我们可以使用数组自带的reverse方法。首先我们使用 split方法将字符串转为数组，然后使用reverse反转字符串，最后使用join方法转为字符串。另外也可以使用数组的reduce方法

给定一个字符串，每个字符需要访问一次。虽然这种情况发生了很多次，但是时间复杂度会正常化为线性。由于没有单独的内部数据结构，空间复杂度是恒定的。

const reverse = string => string.split('').reverse().join('')

const _reverse = string => string.split('').reduce((res,char) => char + res)

2. 回文

回文是一个单词或短语，它的读法是前后一致的。写一个函数来检查。

describe("Palindrome", () => {
 it("Should return true", () => {
  assert.equal(isPalindrome("Cigar? Toss it in a can. It is so tragic"), true);
 })
 it("Should return false", () => {
  assert.equal(isPalindrome("sit ad est love"), false);
 })
})

思考

函数只需要简单地判断输入的单词或短语反转之后是否和原输入相同，完全可以参考第一题的解决方案。我们可以使用数组的 every 方法检查第i个字符和第array.length-i个字符是否匹配。但是这个方法会使每个字符检查2次，这是没必要的。那么，我们可以使用reduce方法。和第1题一样，时间复杂度和空间复杂度是相同的。

const isPalindrome = string => {
  const validCharacters = "abcdefghijklmnopqrstuvwxyz".split("")
  const stringCharacters = string // 过滤掉特殊符号
      .toLowerCase()
      .split("")
      .reduce(
        (characters, character) =>
          validCharacters.indexOf(character) > -1
            ? characters.concat(character)
            : characters,
        []
      );
  return stringCharacters.join("") === stringCharacters.reverse().join("")

3. 整数反转

给定一个整数，反转数字的顺序。

describe("Integer Reversal", () => {
 it("Should reverse integer", () => {
  assert.equal(reverse(1234), 4321);
  assert.equal(reverse(-1200), -21);
 })
})

思考

把number类型使用toString方法换成字符串，然后就可以按照字符串反转的步骤来做。反转完成之后，使用parseInt方法转回number类型，然后使用Math.sign加入符号，只需一行代码便可完成。

由于我们重用了字符串反转的逻辑，因此该算法在空间和时间上也具有相同的复杂度。

const revserInteger = integer => parseInt(number
      .toString()
      .split('')
      .reverse()
      .join('')) * Math.sign(integer)

4. 出现次数最多的字符

给定一个字符串，返回出现次数最多的字符

describe("Max Character", () => {
 it("Should return max character", () => {
  assert.equal(max("Hello World!"), "l");
 })
})

思考

可以创建一个对象，然后遍历字符串，字符串的每个字符作为对象的key，value是对应该字符出现的次数。然后我们可以遍历这个对象，找出value最大的key。

虽然我们使用两个单独的循环来迭代两个不同的输入(字符串和字符映射)，但是时间复杂度仍然是线性的。它可能来自字符串，但最终，字符映射的大小将达到一个极限，因为在任何语言中只有有限数量的字符。空间复杂度是恒定的。

const maxCharacter = (str) => {
    const obj = {}
    let max = 0
    let character = ''
    for (let index in str) {
      obj[str[index]] = obj[str[index]] + 1 || 1
    }
    for (let i in obj) {
      if (obj[i] > max) {
        max = obj[i]
        character = i
      }
    }
    return character
  }

5.找出string中元音字母出现的个数

给定一个单词或者短语，统计出元音字母出现的次数

describe("Vowels", () => {
 it("Should count vowels", () => {
  assert.equal(vowels("hello world"), 3);
 })
})

思考

最简单的解决办法是利用正则表达式提取所有的元音，然后统计。如果不允许使用正则表达式，我们可以简单的迭代每个字符并检查是否属于元音字母，首先应该把输入的参数转为小写。

这两种方法都具有线性的时间复杂度和恒定的空间复杂度，因为每个字符都需要检查，临时基元可以忽略不计。

  const vowels = str => {
    const choices = ['a', 'e', 'i', 'o', 'u']
    let count = 0
    for (let character in str) {
      if (choices.includes(str[character])) {
        count ++
      }
    }
    return count
  }

  const vowelsRegs = str => {
    const match = str.match(/[aeiou]/gi)
    return match ? match.length : 0
  }

6.数组分隔

给定数组和大小，将数组项拆分为具有给定大小的数组列表。

describe("Array Chunking", () => {
 it("Should implement array chunking", () => {
  assert.deepEqual(chunk([1, 2, 3, 4], 2), [[1, 2], [3, 4]]);
  assert.deepEqual(chunk([1, 2, 3, 4], 3), [[1, 2, 3], [4]]);
  assert.deepEqual(chunk([1, 2, 3, 4], 5), [[1, 2, 3, 4]]);
 })
})

一个好的解决方案是使用内置的slice方法。这样就能生成更干净的代码。可通过while循环或for循环来实现，它们按给定大小的步骤递增。

这些算法都具有线性时间复杂度，因为每个数组项都需要访问一次。它们还具有线性空间复杂度，因为保留了一个内部的“块”数组，它与输入数组成比例地增长。

const chunk = (array, size) => {
  const chunks = []
  let index = 0
   while(index < array.length) {
     chunks.push(array.slice(index, index + size))
     index += size
   }
   return chunks
}

7.words反转

给定一个短语，按照顺序反转每一个单词

describe("Reverse Words", () => {
 it("Should reverse words", () => {
  assert.equal(reverseWords("I love JavaScript!"), "I evol !tpircSavaJ");
 })
})

思考

可以使用split方法创建单个单词数组。然后对于每一个单词，可以复用之前反转string的逻辑。

因为每一个字符都需要被访问，而且所需的临时变量与输入的短语成比例增长，所以时间复杂度和空间复杂度是线性的。

const reverseWords = string => string
                                  .split(' ')
                                  .map(word => word
                                                .split('')
                                                .reverse()
                                                .join('')
                                      ).join(' ')

8.首字母大写

给定一个短语，每个首字母变为大写。

describe("Capitalization", () => {
 it("Should capitalize phrase", () => {
  assert.equal(capitalize("hello world"), "Hello World");
 })
})

思考

一种简洁的方法是将输入字符串拆分为单词数组。然后，我们可以循环遍历这个数组并将第一个字符大写，然后再将这些单词重新连接在一起。出于不变的相同原因，我们需要在内存中保存一个包含适当大写字母的临时数组。

因为每一个字符都需要被访问，而且所需的临时变量与输入的短语成比例增长，所以时间复杂度和空间复杂度是线性的。

const capitalize = str => {
  return str.split(' ').map(word => word[0].toUpperCase() + word.slice(1)).join(' ')
}

9.凯撒密码

给定一个短语，通过在字母表中上下移动一个给定的整数来替换每个字符。如果有必要，这种转换应该回到字母表的开头或结尾。

describe("Caesar Cipher", () => {
 it("Should shift to the right", () => {
  assert.equal(caesarCipher("I love JavaScript!", 100), "E hkra FwrwOynelp!")
 })
it("Should shift to the left", () => {
  assert.equal(caesarCipher("I love JavaScript!", -100), "M pszi NezeWgvmtx!");
 })
})

思考

首先我们需要一个包含所有字母的数组，这意味着我们需要把给定的字符串转为小写，然后遍历整个字符串，给每个字符增加或减少给定的整数位置，最后判断大小写即可。

由于需要访问输入字符串中的每个字符，并且需要从中创建一个新的字符串，因此该算法具有线性的时间和空间复杂度。

const caesarCipher = (str, number) => {
  const alphabet = "abcdefghijklmnopqrstuvwxyz".split("")
    const string = str.toLowerCase()
    const remainder = number % 26
    let outPut = ''
    for (let i = 0; i < string.length; i++) {
      const letter = string[i]
      if (!alphabet.includes(letter)) {
        outPut += letter
      } else {
        let index = alphabet.indexOf(letter) + remainder
        if (index > 25) {
          index -= 26
        }
        if (index < 0) {
          index += 26
        }
        outPut += str[i] === str[i].toUpperCase() ? alphabet[index].toUpperCase() : alphabet[index]
      }
    }
  return outPut
}

10.找出从0开始到给定整数的所有质数

describe("Sieve of Eratosthenes", () => {
 it("Should return all prime numbers", () => {
  assert.deepEqual(primes(10), [2, 3, 5, 7])
 })
})

思考

最简单的方法是我们循环从0开始到给定整数的每个整数，并创建一个方法检查它是否是质数。

const isPrime = n => {
  if (n > 1 && n <= 3) {
      return true
    } else {
      for(let i = 2;i <= Math.sqrt(n);i++){
        if (n % i == 0) {
          return false
        }
      }
      return true
  }
}

const prime = number => {
  const primes = []
  for (let i = 2; i < number; i++) {
    if (isPrime(i)) {
      primes.push(i)
    }
  }
  return primes
}

自己实现一个高效的斐波那契队列，欢迎在评论区提交代码

describe("Fibonacci", () => {
 it("Should implement fibonacci", () => {
  assert.equal(fibonacci(1), 1);
  assert.equal(fibonacci(2), 1);
  assert.equal(fibonacci(3), 2);
  assert.equal(fibonacci(6), 8);
  assert.equal(fibonacci(10), 55);
 })
})